Trong hình học, diện tích xung quanh là một trong những khái niệm được sử dụng thường xuyên. Bài viết hôm nay của chúng tôi muốn hướng dẫn các bạn cách tính diện tích xung quanh hình nón – một hình rất phổ biến trong hình học không gian.
Hình nón là gì?
Trước khi biết công thức tính diện tích xung quanh ta cần hiểu hình nón là gì.
Trong hình học không gian, hình nón là hình có một mặt phẳng và một mặt cong hướng lên. Đầu nhọn của hình nón được gọi là đỉnh và bề mặt phẳng được gọi là đáy.
Trong cuộc sống hàng ngày, bạn có thể dễ dàng bắt gặp những đồ vật có hình nón như nón lá, nón kem, nón sinh nhật,… Nó có 3 đặc điểm chính:
- Một đỉnh là một tam giác
- Có 1 mặt tròn làm mặt đáy
- Không có cạnh
Công thức diện tích xung quanh hình nón
Chu vi của một hình nón bao gồm diện tích của mặt xung quanh hình nón, không kể diện tích của đáy.
Diện tích xung quanh hình nón bằng tích của Pi nhân với bán kính đáy nhân với đường sinh của hình nón
Sxq = .rl
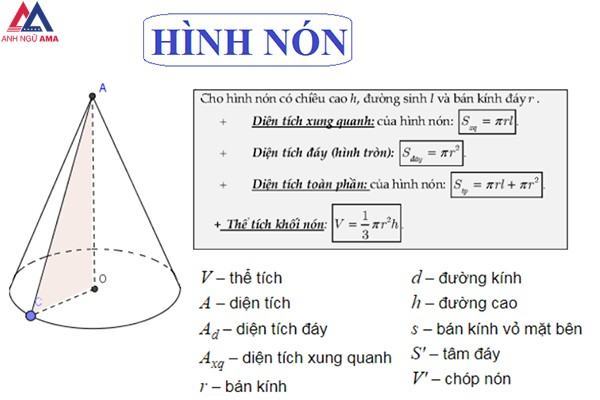Công thức diện tích xung quanh hình nón
Bên trong:
– Sxq là diện tích xung quanh
– là một hằng số, bằng 3,14
– r là bán kính cơ sở
– l là độ dài đường sinh
Hoặc có thể áp dụng công thức sau: “Diện tích xung quanh hình nón bằng nửa tích của chu vi đường tròn đáy với độ dài đường sinh”. Vì một nửa chu vi của hình tròn là π.r.
Ví dụ: Cho một hình nón có đáy là tâm O và đỉnh A. Độ dài bán kính kẻ từ tâm của mặt nón đến một cạnh đáy là 7cm, độ dài đường sinh là 9cm. Diện tích xung quanh hình nón là gì?
Đáp số: Sxq = π.rl = 3,14.7,9= 197,82 (cm)²
Xem thêm tài liệu Toán của Trung Tâm Đào Tạo Việt Á
Công thức của hình nón
Công thức tính diện tích toàn phần của hình nón
Diện tích toàn phần của hình nón bao gồm cả diện tích xung quanh và diện tích đáy tròn. Công thức:
Stp = Sxq + Đáy = .rl + .r^2
Công thức tính thể tích khối nón
Thể tích của hình nón là toàn bộ diện tích mà nó chiếm chỗ, được tính bằng ⅓ tích của diện tích đáy và chiều cao. Đặc biệt:
Hình nón V = .π.r^2.h
Bên trong:
– V là thể tích
– là một hằng số, bằng 3,14
– r là bán kính cơ sở
– h là cao độ từ trên xuống dưới
Diện tích xung quanh hình nón cụt
Hình nón cụt là hình mà một phần của hình nón bị cắt đi. Diện tích xung quanh của một hình nón cụt bao gồm diện tích xung quanh, không bao gồm hai mặt đáy.
Công thức tính chu vi hình nón cụt
Sxq = .(r1+r2).l
Diện tích xung quanh hình nón cụt
Bên trong:
– Sxq là diện tích xung quanh
– là một hằng số, bằng 3,14
– r1, r2 là bán kính 2 đáy
– l là độ dài đường sinh
Tổng diện tích hình nón cụt
Stp = Sxq + S 2 đáy = π.(r1+r2).l + π.(r1)^2 + π.(r2)^2
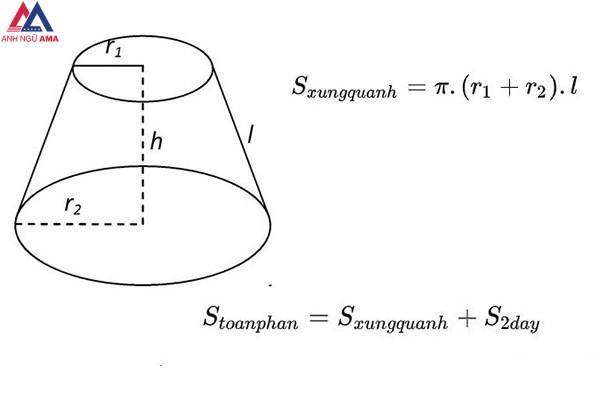Toàn bộ khu vực
Khối lượng của hình nón cụt
V = ⅓.π.h.((r1)^2 + (r2)^2 + r1.r2))
Cách tìm bán kính đáy, đường cao, đường sinh của hình nón
Tìm đường cao của hình nón
Đường cao là độ dài từ tâm của mặt đáy đến đỉnh của hình nón.
Công thức tính chiều cao của hình nón
h^2 = l^2 – r^2
Đường sinh của nón
Đường sinh bằng khoảng cách từ một điểm bất kỳ trên đường tròn đáy đến đỉnh của hình nón.
Độ dài đường sinh của hình nón
l^2 = r^2 + h^2.
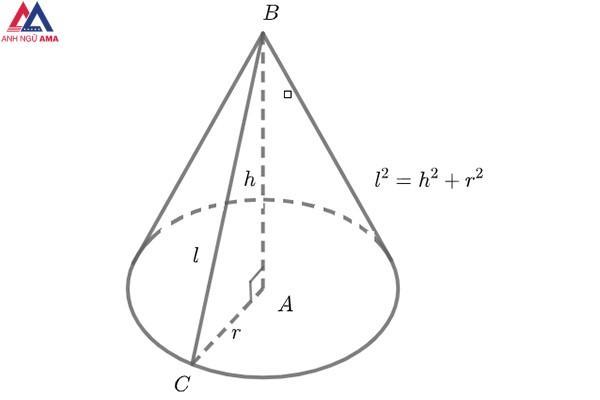chiều dài đường sinh
Bán kính đáy của hình nón
Như chúng ta đã biết, một hình nón được tạo thành khi chúng ta quay một tam giác vuông quanh trục của một trong các góc vuông của nó. Do đó có thể coi bán kính đáy và đường cao là hai góc vuông của tam giác, còn đường sinh sẽ là cạnh huyền. Như vậy khi biết 2 trong 3 dữ liệu này, chúng ta dễ dàng tính toán các dữ liệu còn lại. Đặc biệt:
r^2 = l^2 – h^2
Bài tập tính chu vi hình nón
Bài 1: Một hình nón có bán kính 4cm, chiều cao 7cm, tính chu vi hình nón.
Trong bài tập này, đầu tiên, chúng ta cần tính độ dài đường sinh. Độ dài đường sinh được tính theo công thức:
l^2 = r^2 + h^2
→ l = 8,06cm
Áp dụng công thức diện tích xung quanh hình nón ta có:
Sxq = .rl
= .4.8.06
= 101,23cm2
Bài tập 2: Cho diện tích toàn phần của hình nón là 375 cm. Nếu đường sinh gấp bốn lần bán kính thì đường kính i.đáy nón hoa nhài là bao nhiêu? Sử dụng = 3
Hướng dẫn giải như sau:
Theo đề bài: l = 4r và = 3
Diện tích toàn phần của hình nón là 375 cm2 nên ta có: 3 × r × 4 r + 3 × r2 = 375
<=> 12r2 + 3r2 = 375
<=> 15r2 = 375
=> r = 5
Vậy bán kính đáy của hình nón là 5 => Đường kính của hình nón là 5,2 = 10 cm.
Trên đây là công thức tính diện tích xung quanh hình nón và một số công thức liên quan khác. Theo kinh nghiệm của Trung Tâm Đào Tạo Việt Á, tùy thuộc vào dữ liệu mà câu hỏi đưa ra mà bạn sẽ linh hoạt để tìm ra câu trả lời chính xác.
Bạn thấy bài viết Diện tích xung quanh hình nón: công thức, bài tập ví dụ có đáp ướng đươc vấn đề bạn tìm hiểu không?, nếu không hãy comment góp ý thêm về Diện tích xung quanh hình nón: công thức, bài tập ví dụ bên dưới để vietabinhdinh.edu.vn có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: vietabinhdinh.edu.vn
Nhớ để nguồn bài viết này: Diện tích xung quanh hình nón: công thức, bài tập ví dụ của website vietabinhdinh.edu.vn
Chuyên mục: Giáo dục
Tóp 10 Diện tích xung quanh hình nón: công thức, bài tập ví dụ
#Diện #tích #xung #quanh #hình #nón #công #thức #bài #tập #ví #dụ
Video Diện tích xung quanh hình nón: công thức, bài tập ví dụ
Hình Ảnh Diện tích xung quanh hình nón: công thức, bài tập ví dụ
#Diện #tích #xung #quanh #hình #nón #công #thức #bài #tập #ví #dụ
Tin tức Diện tích xung quanh hình nón: công thức, bài tập ví dụ
#Diện #tích #xung #quanh #hình #nón #công #thức #bài #tập #ví #dụ
Review Diện tích xung quanh hình nón: công thức, bài tập ví dụ
#Diện #tích #xung #quanh #hình #nón #công #thức #bài #tập #ví #dụ
Tham khảo Diện tích xung quanh hình nón: công thức, bài tập ví dụ
#Diện #tích #xung #quanh #hình #nón #công #thức #bài #tập #ví #dụ
Mới nhất Diện tích xung quanh hình nón: công thức, bài tập ví dụ
#Diện #tích #xung #quanh #hình #nón #công #thức #bài #tập #ví #dụ
Hướng dẫn Diện tích xung quanh hình nón: công thức, bài tập ví dụ
#Diện #tích #xung #quanh #hình #nón #công #thức #bài #tập #ví #dụ