Công thức tính đường cao trong tam giác

Bạn đang xem: Công thức tính đường cao trong tam giác – Cách tính đường cao trong tam giác tại vietabinhdinh.edu.vn

Bạn cần tính đường cao trong tam giác nhưng không nhớ công thức tính đường cao trong tam giác. Vậy hãy tham khảo bài viết sau để biết công thức và cách tính đường cao trong tam giác nhé.

Sau đây là công thức tính đường cao trong tam giác, mời các bạn cùng theo dõi.

Đường cao trong tam giác?

Đường cao của tam giác là đoạn vuông góc kẻ từ đỉnh này sang cạnh đối diện. Cạnh đối diện này được gọi là đáy tương ứng với mức cao. Chiều dài của đỉnh là khoảng cách giữa đỉnh và đáy.

Có nhiều cách giúp bạn tính độ cao, một cách đơn giản để tính độ cao trong tam giác là sử dụng công thức Heron:

\[{h_a} = 2\frac{{\sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} }}{a}\]

Trong đó a, b, c là độ dài các cạnh; ha là đường cao vẽ từ đỉnh A đến cạnh BC; p là nửa chu vi:

\[p = \frac{{\left( {a + b + c} \right)}}{2}\]

Công thức tính đường cao trong tam giác đều

Giả sử ABC là tam giác đều cạnh a như sau:

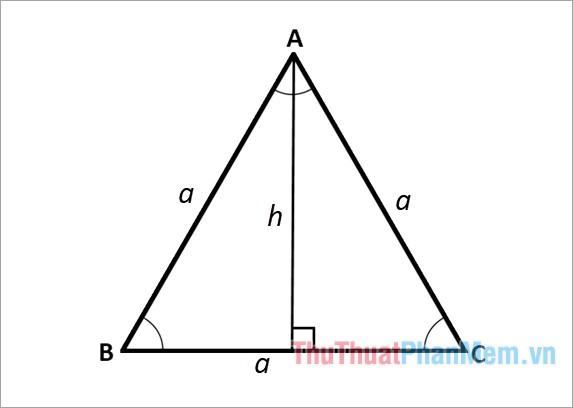
Công thức độ cao: \(h = a\frac{{\sqrt 3 }}{2}\)

Trong đó: h là đường cao của tam giác đều; a là độ dài cạnh của tam giác đều.

Công thức tính đường cao trong tam giác vuông

Giả sử có tam giác vuông ABC vuông tại A như hình vẽ bên:

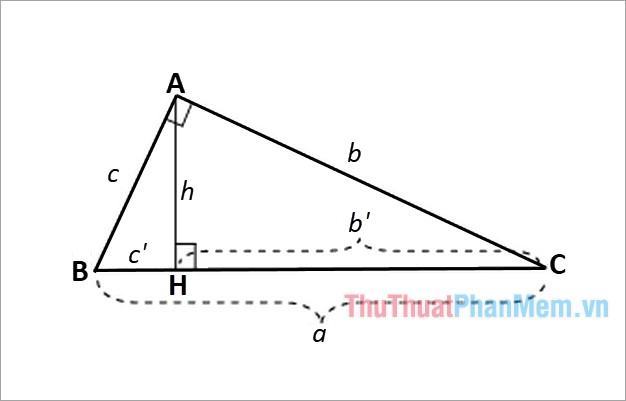
Công thức tính cạnh và chiều cao trong tam giác vuông:

1. \({a^2} = {b^2} + {c^2}\)

2. \({b^2} = a.b’\) và \({c^2} = a.c’\)

3. à = bc

4. \({h^2} = b’.c’\)

5. \(\frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\)

Trong đó: a, b, c lần lượt là các cạnh của tam giác vuông như hình vẽ trên;

b’ là hình chiếu của cạnh b trên cạnh huyền; c’ là hình chiếu của cạnh c lên cạnh huyền;

h là chiều cao của tam giác vuông vẽ từ đỉnh góc vuông A đến cạnh huyền BC.

Như vậy các em có thể dựa vào các công thức tính cạnh và đường cao trong tam giác vuông trên đây để giải toán.

Công thức tính đường cao trong tam giác cân

Giả sử bạn có tam giác ABC cân tại A, đường cao AH vuông góc với H như sau:

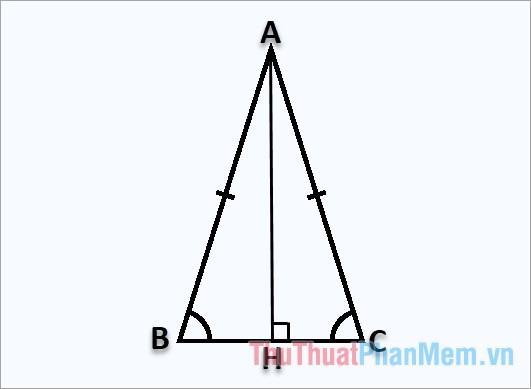
Công thức tính độ cao AH:

Vì tam giác ABC cân tại A nên đường cao AH cũng là trung tuyến nên:

\( \Rightarrow HB = HC = \frac{{BC}}{2}\)

Áp dụng định lý Pitago trong tam giác vuông ABH vuông tại H ta có:

\(A{H^2} + B{H^2} = A{B^2}\)

\( \Rightarrow A{H^2} = A{B^2} – B{H^2}\)

Trên đây là công thức tính đường cao trong tam giác, các bạn chỉ cần tính các thành phần chưa biết trong công thức tính đường cao trong tam giác là có thể tính được đường cao trong tam giác. Chúc may mắn!

Bạn thấy bài viết Công thức tính đường cao trong tam giác – Cách tính đường cao trong tam giác có đáp ướng đươc vấn đề bạn tìm hiểu không?, nếu không hãy comment góp ý thêm về Công thức tính đường cao trong tam giác – Cách tính đường cao trong tam giác bên dưới để vietabinhdinh.edu.vn có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: vietabinhdinh.edu.vn

Nhớ để nguồn bài viết này: Công thức tính đường cao trong tam giác – Cách tính đường cao trong tam giác của website vietabinhdinh.edu.vn

Chuyên mục: Kiến thức chung