Cách tính thể tích hình nón cụt

Bạn đang xem: Cách tính thể tích hình nón cụt tại vietabinhdinh.edu.vn

Bài viết dưới đây chia sẻ với các bạn khái niệm về khối nón cụt, công thức tính thể tích khối nón cụt, cách tính thể tích khối nón cụt và các ví dụ minh họa cụ thể. Nếu bạn đang tìm cách tính thể tích nón cụt chính xác nhất thì hãy tham khảo bài viết dưới đây.

Mời các bạn cùng tìm hiểu khái niệm khối nón cụt và cách tính thể tích khối nón cụt với các ví dụ cụ thể mà bài viết chia sẻ dưới đây.

khái niệm hình nón cụt

Hình nón cụt được tạo từ hình nón như sau: cho tam giác AOC, vuông góc tại O. Khi quay tam giác vuông này quanh cạnh OA ta được một hình nón. Cạnh OC quét đáy tạo thành đường tròn tâm O bán kính OC. Khi đó cạnh AC quét tạo thành đường tròn ngoại tiếp hình nón và cạnh AC gọi là đường sinh của hình nón.

Từ hình nón đã tạo, dùng mặt phẳng song song với mặt đáy cắt qua hình nón ta được hình nón cụt.

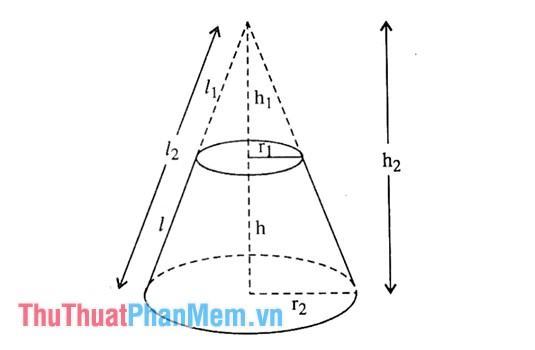
Như vậy, hình nón cụt là hình có đáy là hai hình tròn có bán kính lớn, nhỏ khác nhau, nằm trên hai mặt phẳng song song có tâm là trục đối xứng.

Công thức tính thể tích khối nón cụt

Giả sử ta có một hình nón cụt trong đó r1 và r2 là bán kính hai đáy của hình nón cụt, h là chiều cao và l là độ dài đường sinh.

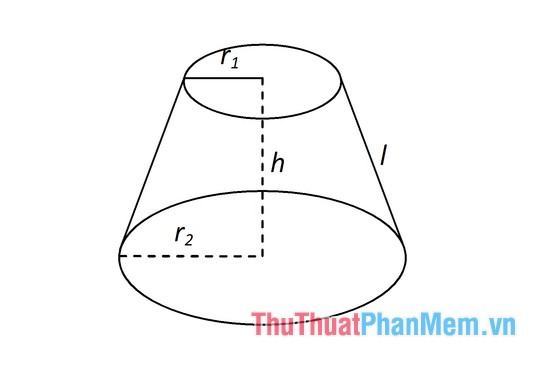
Ta có công thức cho hình nón cụt:

\[V = \frac{1}{3}\pi \left( {{r_1}^2 + {r_2}^2 + {r_1}{r_2}} \right)h\]

Trong đó:

• V là thể tích của khối nón cụt.
• r1, r2: hai bán kính hai đáy của hình nón cụt.
• h : Chiều cao nối hai đáy của hình nón cụt.
• π: số Pi (3,14159265).

Cách tính thể tích khối nón cụt

1. Để tính thể tích khối nón cụt cần dựa vào dữ liệu của bài toán rồi tính r1, r2, h. Nếu có r1, r2, h thì thực hiện bước 2.

2. Sau đó áp dụng công thức tính thể tích khối nón cụt:

\[V = \frac{1}{3}\pi \left( {{r_1}^2 + {r_2}^2 + {r_1}{r_2}} \right)h\]

Và tính kết quả thể tích.

Ví dụ

Xét một hình nón cụt có đường kính đáy lần lượt là 12 cm và 16 cm. Chiều cao nối hai đáy là 7 cm. Tính thể tích của khối nón cụt.

Phần thưởng

Đường kính hai cạnh đáy lần lượt là 12 cm và 18 cm.

Vậy bán kính đáy \({r_1} = \frac{{12}}{2} = 6cm;{r_2} = \frac{{18}}{2} = 9cm;h = 7cm\)

\[V = \frac{1}{3}\pi \left( {{r_1}^2 + {r_2}^2 + {r_1}{r_2}} \right)h\]

\( \Rightarrow V = \frac{1}{3}\pi .\left( {{6^2} + {9^2} + 6.9} \right).7 = \frac{1}{3}\ pi .\left( {36 + 91 + 57} \right).7 = 1253,5c{m^3}\)

Vậy thể tích của hình nón cụt xấp xỉ \(1253,5c{m^3}\)

Trên đây bài viết đã chia sẻ đến các bạn khái niệm về khối nón cụt, công thức tính thể tích khối nón cụt và cách tính thể tích khối nón cụt cùng các ví dụ cụ thể. Hi vọng các bạn sẽ hiểu và áp dụng được cách tính thể tích khối nón cụt chuẩn nhất. Chúc may mắn!

Bạn thấy bài viết Cách tính thể tích hình nón cụt có đáp ướng đươc vấn đề bạn tìm hiểu không?, nếu không hãy comment góp ý thêm về Cách tính thể tích hình nón cụt bên dưới để vietabinhdinh.edu.vn có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: vietabinhdinh.edu.vn

Nhớ để nguồn bài viết này: Cách tính thể tích hình nón cụt của website vietabinhdinh.edu.vn

Chuyên mục: Kiến thức chung