Cách tính diện tích tam giác nhanh và chuẩn nhất

Bạn đang xem: Cách tính diện tích tam giác nhanh và chuẩn nhất tại vietabinhdinh.edu.vn

Tính diện tích tam giác là bài toán mà các em thường gặp ở bậc tiểu học, với mỗi trường hợp đặc biệt của tam giác sẽ có một cách tính diện tích khác nhau. Bài viết dưới đây hướng dẫn các bạn cách tính diện tích tam giác thường, tam giác vuông, tam giác cân và tam giác đều giúp các bạn giải mọi bài toán.

1. Công thức tính diện tích tam giác thường

Để tính diện tích của một tam giác bình thường, bạn có thể sử dụng các công thức sau:

1) \({S_{ABC}} = \frac{1}{2}ah\)

Trong đó:

– a là độ dài một trong ba cạnh của tam giác.

– h là độ dài đường cao tương ứng vẽ từ đỉnh đối diện với cạnh đáy có độ dài a.

Ví dụ: Tìm diện tích tam giác ABC có cạnh đáy BC = 4 cm và độ dài đường cao kẻ từ đỉnh A là 16 cm. Tính diện tích tam giác ABC.

Giải: Tam giác ABC có đường cao nằm ngoài tam giác. Diện tích tam giác vẫn được tính theo công thức: \({S_{ABC}} = \frac{1}{2}.4.16 = 32\left( {c{m^2}} \right)\ )

2) \({S_{ABC}} = \frac{1}{2}ab\sin C = \frac{1}{2}ac\sin B = \frac{1}{2}bc\sin A\ )

Diện tích của một tam giác bằng nửa tích của hai cạnh kề và sin của góc tạo bởi hai cạnh đó trong tam giác.

Ví dụ: Tìm diện tích tam giác ABC biết AB = 8cm, BC = 6cm, góc B bằng 60 độ.

Giải: Theo công thức tính diện tích tam giác ta có:

\[{S_{ABC}} = \frac{1}{2}a.b.\sin C = \frac{1}{2}.8.6.\sin 30 = \frac{1}{2}.48.\frac{1}{2} = 12\left( {c{m^2}} \right)\]

3) Công thức Heroon

\({S_{ABC}} = \sqrt {p(p – a)(p – b)(p – c)} \)

Công thức Hêrôin – p là nửa chu vi tam giác, a, b, c là độ dài ba cạnh của tam giác.

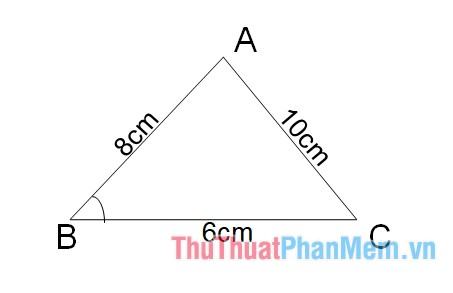
Ví dụ: Cho tam giác ABC có độ dài các cạnh AB=8cm, BC=6cm, AC=10cm. Tính diện tích tam giác ABC.

Phần thưởng

Chu vi tam giác ABC là: \({P_{ABC}} = \left( {8 + 6 + 10} \right) = 24\) cm

Vậy nửa chu vi tam giác là 12

Theo công thức Heron diện tích tam giác ABC là:

\[{S_{ABC}} = \sqrt {12\left( {12 – 8} \right)\left( {12 – 6} \right)\left( {12 – 11} \right)} = \sqrt {288} \approx 16,97c{m^2}\]

4) \({S_{ABC}} = pr\)

(p là nửa chu vi tam giác, r là bán kính đường tròn nội tiếp tam giác)

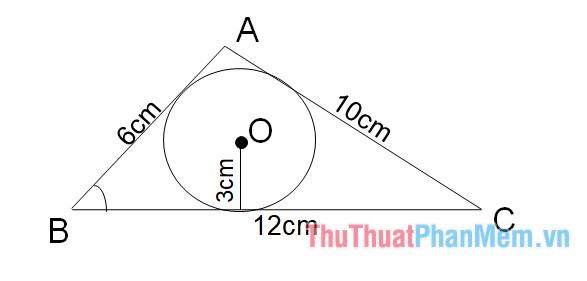
Ví dụ, cho tam giác ABC, chu vi của tam giác là 28 cm. Bán kính đường tròn ngoại tiếp tam giác là 3cm. Tính diện tích tam giác.

Phần thưởng

Nửa chu vi tam giác là 28/2=14cm

Diện tích tam giác ABC là: \({S_{ABC}} = pr = 14.3 = 42c{m^2}\)

* Một số lưu ý khi tính diện tích tam giác.

Cho một tam giác chứa góc bẹt là đường cao ngoại tiếp tam giác.

– Khi tính diện tích hình tam giác, chiều cao nào ứng với đáy đó.

– Nếu 2 tam giác có cùng chiều cao hoặc bằng nhau -> diện tích 2 tam giác tỉ lệ với 2 đáy và ngược lại nếu 2 tam giác có chung đáy (hoặc 2 đáy bằng nhau) -> diện tích tam giác tỉ lệ với 2 đáy tương ứng độ cao.

2. Công thức tính diện tích tam giác vuông

Công thức tính diện tích tam giác vuông:

\({S_{ABC}} = \frac{1}{2}ab\) (trong đó a, b là độ dài hai cạnh của góc vuông)

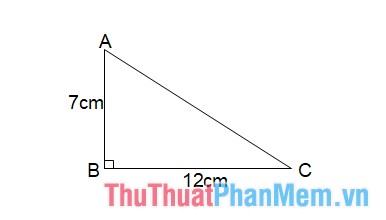
Ví dụ: Tam giác ABC vuông tại B, độ dài cạnh AB = 7 cm, cạnh BC = 12 cm. Tính diện tích tam giác ABC.

Giải: Dựa vào công thức tính diện tích tam giác vuông, ta có:

\[{S_{ABC}} = \frac{1}{2}.AB.BC = \frac{1}{2}.7.12 = 42\left( {c{m^2}} \right)\]

3. Công thức tính diện tích tam giác cân

\({S_{ABC}} = \frac{1}{2}ah\) (Trong đó a là độ dài cạnh đáy có thể là một trong ba đáy, h là độ dài đường cao tương ứng với đỉnh đối diện với đáy có độ dài a)

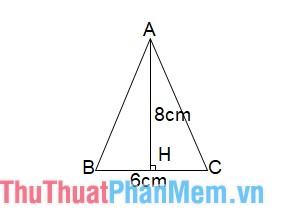
Ví dụ: tam giác ABC cân tại A, chiều cao AH là 8cm, cạnh đáy BC là 6cm

=> Diện tích tam giác ABC:

\[{S_{ABC}} = \frac{1}{2}.8.6 = 24\left( {c{m^2}} \right)\]

4. Công thức tính diện tích tam giác đều

\({S_{ABC}} = {a^2}.\frac{{\sqrt 3 }}{4}\) (trong đó a là độ dài cạnh của tam giác)

Ví dụ Tính diện tích tam giác đều ABC biết độ dài cạnh AB = 8cm.

Giải: Theo công thức tính diện tích tam giác đều, ta có:

\[{S_{ABC}} = {a^2}.\frac{{\sqrt 3 }}{4} = {8^2}.\frac{{\sqrt 3 }}{4} = 16\left( {c{m^2}} \right)\]

Trên đây là công thức tính diện tích tam giác vuông, tam giác vuông, tam giác cân, tam giác đều giúp các em dễ dàng làm bài tập. Chúc may mắn.

Bạn thấy bài viết Cách tính diện tích tam giác nhanh và chuẩn nhất có đáp ướng đươc vấn đề bạn tìm hiểu không?, nếu không hãy comment góp ý thêm về Cách tính diện tích tam giác nhanh và chuẩn nhất bên dưới để vietabinhdinh.edu.vn có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: vietabinhdinh.edu.vn

Nhớ để nguồn bài viết này: Cách tính diện tích tam giác nhanh và chuẩn nhất của website vietabinhdinh.edu.vn

Chuyên mục: Hình Ảnh Đẹp